BAB III ( Bola Pejal)

           
           Bola Pejal

Momen inersia

Benda	Poros	Gambar	Momen inersia
Batangsilinder	Pusat		${\displaystyle I={\frac {1}{12}}\,\!mL^{2}}$
Batang silinder	Ujung		${\displaystyle I={\frac {1}{3}}\,\!mL^{2}}$
Silinder berongga	Melalui sumbu		${\displaystyle I=mR^{2}}$
Silinder pejal	Melalui sumbu		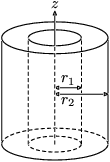${\displaystyle I={\frac {1}{2}}\,\!mR^{2}}$
Silinder pejal	Melintang sumbu		${\displaystyle I={\frac {1}{4}}\,\!mR^{2}+{\frac {1}{12}}\,\!mL^{2}}$
Bolapejal	Melalui pusat		${\displaystyle I={\frac {2}{5}}\,\!mR^{2}}$
Bola pejal	Melalui salah satu garis singgung		${\displaystyle I={\frac {7}{5}}\,\!mR^{2}}$
Bola berongga	Melalui diameter		${\displaystyle I={\frac {2}{3}}\,\!mR^{2}}$

Batang Homogen

a. Poros berada di Pusat

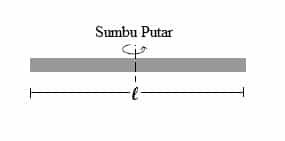
I = 1/12m.l2

Keterangan :
I = momen inersia (kg m2)
l = panjang batang (m)
m = massa (kg)

b. Poros berada di salah satu ujung

I = 1/3m.l2

Keterangan:
I = momen inersia (kg m2)
l = panjang batang (m)
m = massa (kg)

c. Poros Bergeser

I = 1/12 m.l2 + m.(k.l)2
Keterangan:
I = momen inersia (kg m2)
l = panjang batang (m)
k.l = panjang pergeseran (m)
m = massa (kg)

Benda Berbentuk Silinder

a. Silinder Pejal
I = 1/2 m.R2
Keterangan
I = momen inersia (kg m2)
R = jari-jari silinder (m)
m = massa (kg)

b. Silinder Tipis Berongga
I = m.R2

Keterangan
I = momen inersia (kg m2)
R = jari-jari silinder (m)
m = massa (kg)

c. Silinder Berongga Tidak Tipis

I = 1/2 m (R12 + R22)

I = momen inersia (kg m2)
R1 = jari-jari dalam silinder (m)
R2 = jari-jari luar silinder (m)
m = massa (kg)

Benda Berbentuk Bola

a. Bola Pejal

I = 2/5m.R2

Keterangan:
I = momen inersia (kg m2)
R = jari-jari bola(m)
m = massa (kg)

b. Bola Berongga

I = 2/3m.R2

Keterangan
I = momen inersia (kg m2)
R = jari-jari bola(m)
m = massa (kg)

Contoh : 

Perhatikan gambar dibawah ini!

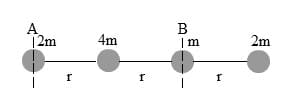
Terdapat empat buah partikel yang dihubungkan oleh sebuah batang yang massanya diabaikan. Tentukan momen inersia sistem partike jika :
a. Diputar terhadap poros A
b. Diputar terhadap poros B

Pembahasan:
a. Diputar terhadap poros A

I = Ʃm.R2
I = 2m(0)2 + 4m (r)2 + m (2r)2 + 2m (3r)2
I = 0 + 4m r2 + 18m r2
I = 26m r2

b. Diputar terhadap poros B

I = Ʃm.R2
I = 2m (2r)2 +4m (r)2 + m (0)2 + 2m (r)2
I = 8m r2 + 4m r2 + 0 + 2m r2
I = 14 m r2

2. Diketahui sebuah batang homogen bermassa 0,6 kg dan panjang 60 cm. Apabila gumpalan lumpur bermassa 20 gram dilempar dan menempel pada salah satu ujung batang, maka tentukan momen inersia sistem melalui pusat batang.

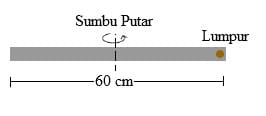
Pembahasan:

I = 1/12m.l2 + mR2
I = 1/12(0,6).(0,6)2 + 0,02(0,3)2
I = 0,018 + 0,0018
I = 0,0198
I = 1,98 x 10-2 kg m2

3. Apabila sebuah silinder pejal bermassa 2 kg dan berjari-jari 0,1 m diputar melalyi sumbu silinder dan segumpal lumpur bermassa 0,2 kg menempel pada jarak 0,05 meter dari pinggir silinder, maka hitunglah momen inersia sistem.

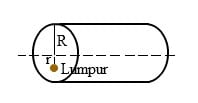
Pembahasan:

I = I silinder + I lumpur
I = 1/2 mR2 + m.r2
I = 1/2 (2).(0,1)2 + 0,2. (0,05)2
I = 0,01 + 0,0005
I = 0,0105
I = 1,05 x 10-2 kg m2